The Distributive Property of Roulette Betting

If you're the type of person who likes to spread their bets around the Roulette table, you should know about the Distributive Property of Roulette Betting. It can save you a lot of time, hassle, and awkwardness if your bets can be consolidated into larger multi-number bets.

What is the Distributive Property of Roulette Betting?

The Distributive Property of Roulette Betting states

Every multi-number bet (besides the 5-number bet) can be reconstructed by distributing the bet amount equally amongst the numbers covered by the original bet.

or in other words

Betting $X on an n-number bet is equivalent to betting \($X \over n\) each of the n numbers Straight-up.

which can be represented formulaically as

\({$X \times Payout_n} \equiv n \times {$X \over n} \times Payout_1 \)

Where \(\color{#8acdd8}Payout_n\) is the payout multiplier for an n-number bet (when \(n \neq 5\)).

And this is true for all variations of Roulette, including single-zero, double-zero, and even the horrendous triple-zero wheel.

So betting $6 on the 6-number "Double Street" is equivalent to making six $1 bets on each of the covered numbers individually.

These two betting configurations are equivalent.

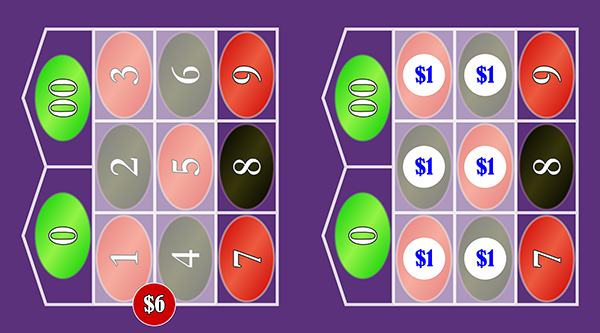
Does this really work?

If we look at the two sets of wagers above, we can easily see that hitting any number outside of - will result in a $6 loss. But what happens when we hit a number between and ?

With the single $6 Double Street bet, we win 5-to-1, for a net win of +$30.

With the six $1 Straight-up bets, we will lose five of the $1 bets, but one will win $35, for a net win of +$30.

So in both scenarios, we lose $6 when we miss and win +$30 when we hit.

This property works with any combination of bets where the bets are all uniform. You can consolidate three Straight-up bets into a 3-number Street bet. You can consolidate four Straight-up bets into one 4-number Corner bet. You can even consolidate two Street bets into a single Double Street bet.

These are all equivalent decompositions of the $6 Double Street bet.

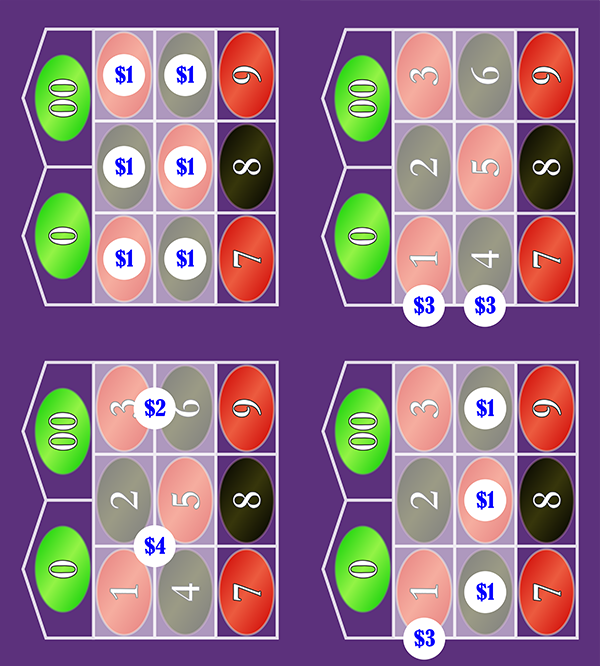
The only bet where this property does not apply is the 5-number "Basket" bet, which is a bet on the numbers , , , , and .

Terminology

If you've never heard of the Distributive Property of Roulette Betting, it's probably because I literally just made it up. Recently, I've been analyzing Roulette betting systems and noticed how a lot of them waste time by making you sprinkle bets needlessly all over the layout. I've never seen this property formally discussed anywhere, so I thought I'd just give it a formal name.

I named it the Distributive Property because you're just taking the multi-number bet and distributing it equally across the single-number bets.

Hopefuly, you've already read my post on the Basics of Roulette Math. In that post, I cover the names of all the multi-number bets, so if you're not familiar with them, please read that post first.

Before I explain how this all works, let's go over some of the other terms involved in this property.

Distribution/Decomposition

Distribution or Decomposition is taking a multi-number bet and breaking it down into smaller bets, often a series of "Straight-up" single-number bets.

It's also possible to distribute a multi-number bet into smaller multi-number bets. For example, a $12 Double Street bet can be split into two $6 Street bets. Or it could be split into a $6 Street bet and three $2 Straight-up bets. Or it could be split into an $8 Corner bet and a $4 Split bet.

You can break down a multi-number bet in many different ways.

Consolidation

Consolidation is "rolling-up" individual bets into a single bet with the same win/loss characteristics. A typical consolidation is taking n number of $X Straight-up bets into a single $nx n-number bet. For example, rolling up four $2 bets into a single $8 Corner bet.

Density

Density or Betting Density is the bet amount per spot once a multi-number bet has been fully distributed to single-number bets. You can also think of this as the equity per spot.

In order for two betting scenarios to be equivalent, their betting density must be equal for the covered area. For example, you can bet $6 on the - Double Street, but that would have a different density compared to betting $3 on the , , , Corner Bet in conjunction with a $3 , Split Bet. This implies that the two betting schemes are not equivalent and will pay out differently when the numbers hit.

For two betting schemes to be equivalent, their densities must be consistent. In this example, the $3 + $3 bets are unevenly spread out even though the total amount bet is the same. The overall payout will be higher if you hit the or (+$48) over hitting the , , , or , (+$21). With the $2 + $4 bets, the payout is consistently+$30, which is identical to the payout for the $6 Double Street bet.

What is this Sorcery?

This all magically works out because all Roulette bets (besides that pesky 5-number bet) have the same horrible house edge (5.26% for double-zero!). This means if you bet the same amount on n spots, your Expected Value (EV) should be exactly the same if you bet that same amount on an n-number bet.

And we can prove this mathematically using one of the formulas I introduced in my post on the Basics of Roulette Math. The payout for every bet in Roulette (besides the 5-number bet) can be calculated by using the formula:

$$ { Payout_n } = { {36 - n} \over n } $$

So an $n wager on an n-number bet can be calculated as

\begin{align} n \times { Payout_n } & = { n \times { {36 - n} \over n } } \\ \\ & = 36 - n \\ \\ & = 36 - 1 - n + 1 \\ \\ & = { {36 - 1} \over 1 } - (n - 1) \\ \\ & = { Payout_1 } - (n - 1) \\ \end{align}

Which is the win from a single $1 Straight-up bet minus the (n-1) losses from the losing Straight-up bets.

For example, if you bet $1 on 12 numbers Straight-up, then one of those bets will win $35 and 11 of those bets will lose, for a net win of $24, which is what your 2-to-1 payout would be for betting $12 on a dozen or column.

\begin{align} $12 \times { Payout_{12} } & = { Payout_1 } - (12 - 1) \\ \\ $12 \times 2 & = $35 - $11 \\ \\ $24 & = $24 \\ \end{align}

Here's the formula applied to all 7 bet types (without the 5-number bet):

n	Amount Bet	Consolidated Bet Type	Consolidated Bet Payout	Distributed Bet Payout
18	$18	Even Money	1:1 = +$18	$35 - 17 = +$18
12	$12	Dozens/Columns	2:1 = +$24	$35 - 11 = +$24
6	$6	Double Streets	5:1 = +$30	$35 - 5 = +$30
4	$4	Corners	8:1 = +$32	$35 - 3 = +$32
3	$3	Streets	11:1 = +$33	$35 - 2 = +$33
2	$2	Splits	17:1 = +$34	$35 - 1 = +$34
1	$1	Straight-Up	35:1 = +$35	$35 - 0 = +$35

Where n is the number of bets covered and the Betting Density is $1 per spot.

How can I make use of the Distributive Property of Roulette Betting?

I've been watching a lot of Roulette system reviews on CEG Dealer School's YouTube Channel, and I've noticed that the systems submittied by viewers are often impractical when it comes to betting at a brick and mortar casino.

These systems may seem enjoyable on paper or even tapping your finger on a Roulette iPad app, but it's often extremely impractical to bet on spots all over a real-world table, since you may have to reach over other people.

If you can consolidate your bets using the Distributive Property of Roulette Betting, you can often save time and prevent yourself from awkwardly reaching over other people. On a Roulette table, reach-arounds are a bad thing.

Case Study: "Diamond Heist"

In CEG Dealer School's review of the system named "Diamond Heist", they bet $30 across 6 Corner bets that are spread evenly across the first two columns. They could have just put $15 on Column 1 and $15 on Column 2, saving time and the dreaded "reach around" - stretching their arms awkwardly across the felt and annoying other players.

A few days ago, The CEG Dealer School reviewed a Roulette system named "Diamond Heist", where they made 6 Corner bets that covered the entire first two columns. For the purposes of this post, we're going to ignore the other bets involved in this system.

The 6 bets in question in the "Diamond Heist" Roulette system.

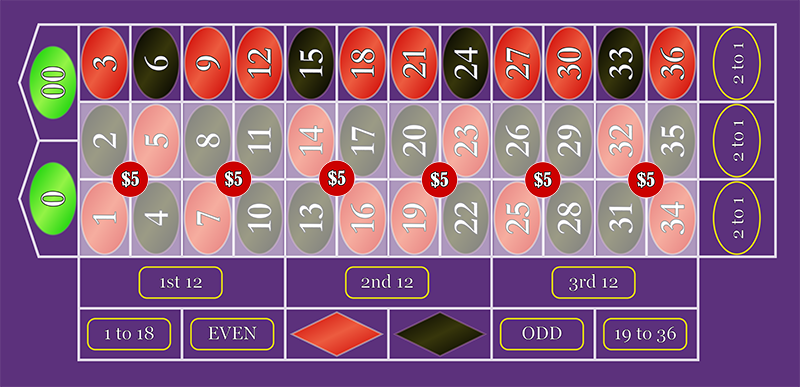
There is $30 covering the first two columns evenly. This is the perfect candidate for consolidation! Instead of these 6 bets, we can place $15 on each of the first two columns.

It's easier to make two $15 on one side of the felt rather than spread $30 all across the table, especially when the table is full.

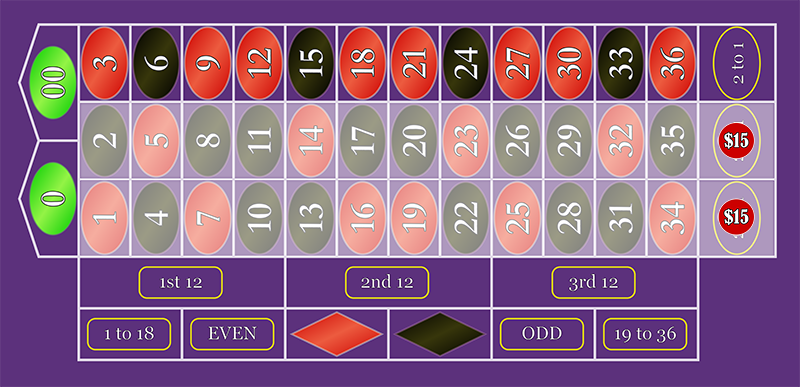
Hitting one of the Corner bets in the original system pays $40, but you lose $25 in the other Corner bets, for a net gain of +$15.

Hitting one of the Column bets in the modified system pays $30, but you lose $15 on the other column bet, for a net gain of +$15.

With the two column bets, you've concentrated your bets to one small section of the field, instead of stretching across 2/3 of the inside betting area.

Case Study: "Not too Low, Not too High"

The "Not too Low, Not too High" system has even more opportunities to consolidate your bets.

The CEG Dealer School crew also reviewed another system called "Not too Low, Not too High", which has even more opportunities to consolidate.

This is the original version of the "Not too Low, Not too High" system, with three sets of three $10 Splits that can be consolidated into three $30 Double Street bets.

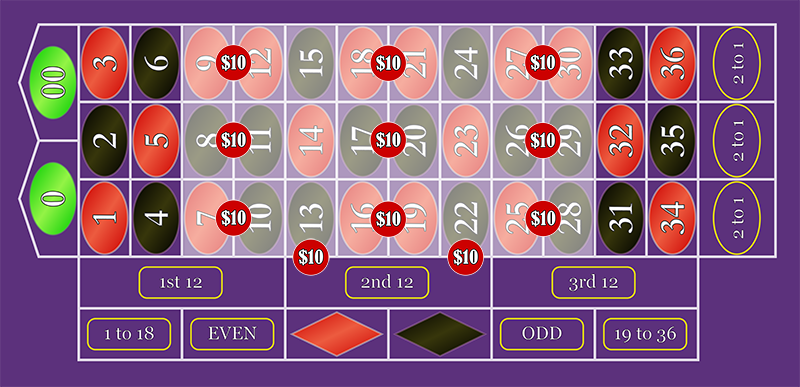
In this system, all the Split bets can be rolled up into three $30 Double Street bets.

The $30 - Double Street bet can then be redistributed into two $15 Street bets. Then the four Street Bets in the middle ($10, $15, $15, and $10) can be consolidated by taking $10 of each bet and rolling it up into a single $40 bet on the 2nd Dozen, leaving two $5 Street Bets in the middle two Streets. These are finally rolled up into a $10 - Double Street bet, and we have reached our final form.

Instead of making 11 bets covering 2/3 of the inside layout, we've consolidated the bets into 4 bets along the inside/outside edge.

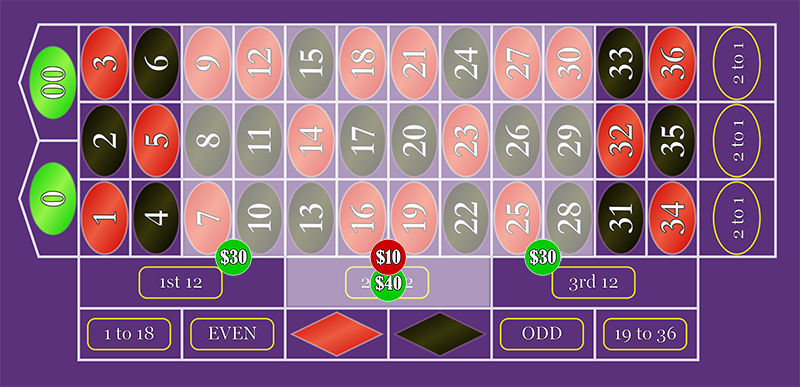
If you check the payouts, you'll find that they are identical to the original system. You get paid +$10 for the - Street and the - Street and +$70 for the rest of the covered numbers.

We've saved ourselves some time and we've eliminated the awkward "reach-around"! This is what the Distributive Property of Roulette Betting is all about!

But wait, there's more!

If you're an experienced Roulette player, most of this may seem obvious. However, if you're new to Roulette, this may be a revelation to you.

Even though decomposing a bet may not always be possible because of table limits or chip denominations, just knowing that splitting up a bet would not affect your win/loss results is enough for us to move onto more complicated topics.

In the future we will discuss how we can use the Distributive Property of Roulette Betting to do more than just save time and avoid awkwardness. We will use it to discover ways to reduce your negative expected loss to the house.